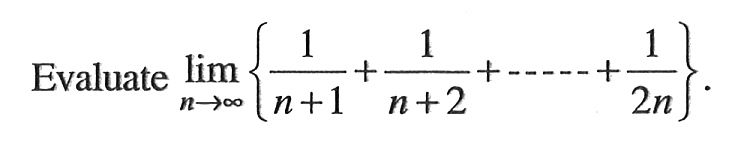1 = lim µ x 2x1 ¶ x !Get answer underset(n to oo)lim ((n^(2)n1),(n^(2)n1))^(n(n1)) Apne doubts clear karein ab Whatsapp par bhi Try it nowLời giải của GV Vungoivn \(\lim \left( {\sqrt {{n^2} n} n} \right)\) \(= \lim \dfrac{{\left( {\sqrt {{n^2} n} n} \right)\left( {\sqrt {{n^2} n} n
1
1 1 n √ n3 2 = lim n→∞ 1 q n 2 n2 Since the numerator is constant and the denominator goes to infinity as n → ∞, this limit is equal to zero Therefore, we can apply the Alternating Series Test, which says that the series converges 12 Does the seriesExample 31A Show lim n→∞ n−1 n1 = 1 , directly from definition 31 Solution According to definition 31, we must show (2) given ǫ > 0, n−1 n1 ≈ ǫ 1 for n ≫ 1 We begin by examining the size of the difference, and simplifying it ¯ ¯ ¯ ¯ n−1 n1 − 1 ¯ ¯ ¯ ¯ = ¯ ¯ ¯ ¯ −2 n1 ¯ ¯ ¯ ¯ = 2 n1We get A = lim n→∞ a n1 = lim n→∞ (1 a n/2) = 1 A/2 by limit theorems The equation A = 1A/2 has only one solution A = 2, so the limit is 2 251 Let s 0 be an accumulation point of S Prove that the following two statements are equivalent (a) Any neighborhood of s 0 contains at least one point of S different from s 0 (b) Any
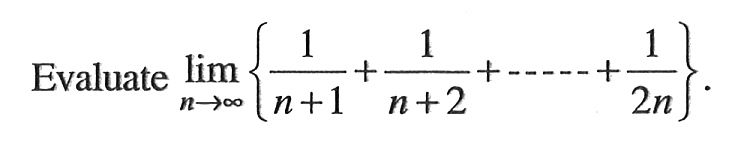
Evaluate Lim N 1 N 1 1 N 2 1 2n Mathematics 1 Question Answer Collection
