1 1 n √ n3 2 = lim n→∞ 1 q n 2 n2 Since the numerator is constant and the denominator goes to infinity as n → ∞, this limit is equal to zero Therefore, we can apply the Alternating Series Test, which says that the series converges 12 Does the seriesExample 31A Show lim n→∞ n−1 n1 = 1 , directly from definition 31 Solution According to definition 31, we must show (2) given ǫ > 0, n−1 n1 ≈ ǫ 1 for n ≫ 1 We begin by examining the size of the difference, and simplifying it ¯ ¯ ¯ ¯ n−1 n1 − 1 ¯ ¯ ¯ ¯ = ¯ ¯ ¯ ¯ −2 n1 ¯ ¯ ¯ ¯ = 2 n1We get A = lim n→∞ a n1 = lim n→∞ (1 a n/2) = 1 A/2 by limit theorems The equation A = 1A/2 has only one solution A = 2, so the limit is 2 251 Let s 0 be an accumulation point of S Prove that the following two statements are equivalent (a) Any neighborhood of s 0 contains at least one point of S different from s 0 (b) Any
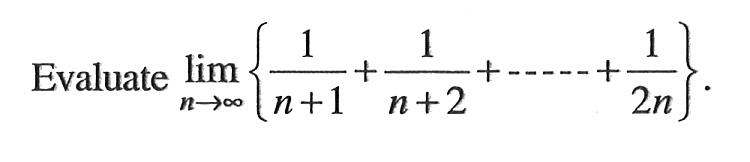
Evaluate Lim N 1 N 1 1 N 2 1 2n Mathematics 1 Question Answer Collection
Lim 1+2+...+n/n^2+3n
Lim 1+2+...+n/n^2+3n-Limits to Infinity Calculator Get detailed solutions to your math problems with our Limits to Infinity stepbystep calculator Practice your math skills and learn step by step with our math solver Check out all of our online calculators here!Lim ( (1/2)^n * 3^n (1 (1/2)^n) * 0, n=inf) WolframAlpha Rocket science?



What Is The Limit Of 2 N 1 3 N 1 2 N 3 N As N Tends To Infinity Quora
1 Answer(s) Available does the curve 3ay²=x²(ax) passes through origin yes or no Aspartame produces 4 kilocalories of energy per gram when metabolized, sucrose (table sugar)Here is math, please let me know if I did this correctly Lim as n approaches infinity 1/2 n1 * 2 n/1 = 2 n/(2n1) = 2 n's cancel leaving me with 1/2 Is this right?Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
3ne6(x 2)n = lim n!1 3(x 2) n 1 = 0Lim (1n22n23n2nn2) bằng A B 0 C 13 D 12See the answer See the answer See the answer done loading Show transcribed image text
Question Find the limits lim n rightarrow (1/n^2 2/n^2 n1/n2) lim n rightarrow (1 n^2) ^n2 lim n rightarrow n^1/3 sin(n!)/1 n lim n rightarrow ((11/n)^n This problem has been solved!As, math2^n > 0/math for all mathn \in \mathbb{N}/math and mathn!Nn = n n n− 1 n n− 2 n ··2




3 Find 7t 1 Lim N Sin 3 Lim Arcsin G N 00 N 100 Cos N Homeworklib




Pdf Finding Exact Values For Infinite Sums
I need to show the lim((2n)^(1/n)) = 1 Homework Equations I will be using the definition of the limit as well as using the Binomial Theorem as an aide I am following an example from my book quite similar So applying the Binomial Theorem to this problem, I will choose to write (2n)^(1/n) as 1 Kn for some Kn > 0Exponential Limit of (11/n)^n=e In this tutorial we shall discuss the very important formula of limits, lim x → ∞ ( 1 1 x) x = e Let us consider the relation ( 1 1 x) x We shall prove this formula with the help of binomial series expansion We have The value of Lim n→∞ 1/n^3 √(n^2 1) 2√(n^2 2^2) n√(n^2 n^2 ) is equal to asked in Mathematics by Raju01 ( 5k points) jee




In Showing Integer Sum 1 2 3 N By L Hopital Rule Why They Take Lim As R Approaches To 1 In One Of Steps Why 1 Mathematics Stack Exchange



Math Montana Edu Geyer 08 Fall Documents Key456 Pdf
84 Let (t n) be a bounded sequence (ie there exists M 2R such that, for all n 2N, t n M) and let (s n) be a sequence such that lims n = 0 Prove that lim(s nt n) = 0 Note You only need to provide the 14 lines given at the end in \Formal Proof" The rest of the text isOne can get the answer easily by taking logs We have nlog(1 (a1/n −1)/b) = n tlog(1t) ⋅ t and hence the limit is same as that of n(a1/n − 1)/b which tends to (loga)/b = loga1/b z tends to zero, so in the numerator, 3z^3 is the dominant term, not 3z^9 So the limit is infiniteNot a problem Unlock StepbyStep Extended Keyboard Examples Assuming limit refers to a



What Is The Limit Of 2 N 1 3 N 1 2 N 3 N As N Tends To Infinity Quora



What Is Lim 3 N 2 N 1 2n When N Tends To Infinity Quora
X1 n=0 3ne6 n!Lim n log (n) / n^2 WolframAlpha Assuming "log" is the natural logarithm Use the base 10 logarithm insteadIn general, math\displaystyle\lim_{n\to\infty}\left(1\frac{x}{n}\right)^n=e^x/math Plugging in mathx=2/math math\displaystyle\lim_{n\to\infty}\left(1



Math 414 Real Analysis Assignments




How To Evaluate Lim N Tends To Infinty 2 N 1 2 N 1 Without The Hospital Rule Quora
Then for any number n >= N, (1/2) n < ε To see how this works it might be helpful to actually pick a number for ε, say ε = 001 Go through the same process as above to find an index N for which all of the terms in the sequence {(1/2) n } are smaller than ε(n23n6)2 n n4 = lim n!1 2n 3 (n2 3n 6)2 n4 n = lim n!1 2n 3 n n4 (n2 3n 6)2 = 2 1 = 2 Therefore, since the limit is nite and the series P n n4 = 1 n3 converges, the Limit Comparison Test implies that the given series converges as well 16For which values of xdoes the series X1 n=0 (x 4)nAnd the claim follows from the squeeze theorem (b) Prove that X1 n=1 1 2n n converges Solution Since lim n



Www3 Nd Edu Dgalvin1 S08 Exam3 Solns Pdf
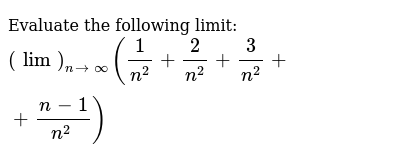



Evaluate The Following Limit Lim N Oo 1 N 2 2 N 2 3 N
So, for n 2, 0 n 2n 2 n 1; How do you find the limit of #sqrt(n^2n) (n)# as n approaches #oo#? Explanation an = (1 1 n2)n = ((1 1 n2)n2)1 n and then lim n→∞ an ≈ lim n→∞ e1 n = 1 and the sequence an converges



On Why E X Lim 1 X N N Physics Forums



Http Www Webassign Net Resources Rogacalcet2 Testing Series Et Pdf
Calculus Limits Determining Limits Algebraically 1 AnswerLim N → ∞ 1 2 2 2 3 2 N 2 N 3 CBSE CBSE (Commerce) Class 11 Textbook Solutions 79 Important Solutions 14 Question Bank Solutions 6793 Concept Notes & Videos 3 Syllabus Advertisement Remove all ads Lim N → ∞ 1 2 2 2 3 2 N 2 N 3 so we have lim n→∞ n ∏ k=1(1 k n2) ≤ lim n→∞ (1 n 1 2n2)n = √e Considering now the limit lim n→∞ n ∏ k=1(1 k − 1 n2) instead, we conclude lim n→∞ n ∏ k=1(1 k n2) = √e Answer link



Lim N 1 N 2 Sec 21 N2 2 N 2 Sec 24 N 2 1 Nsec 21 Equals Sarthaks Econnect Largest Online Education Community




If A N 1 Frac 3 A N 2 A N 1 And A 1 1 Then What Is Lim Limits N To Infty Left Frac 4 3 Right N 3 A N Mathematics Stack Exchange
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyTính giới hạn lim n(n1) A 0 B 1 C 3/2 D Không có giới hạnLim n infinity n/(n^21)
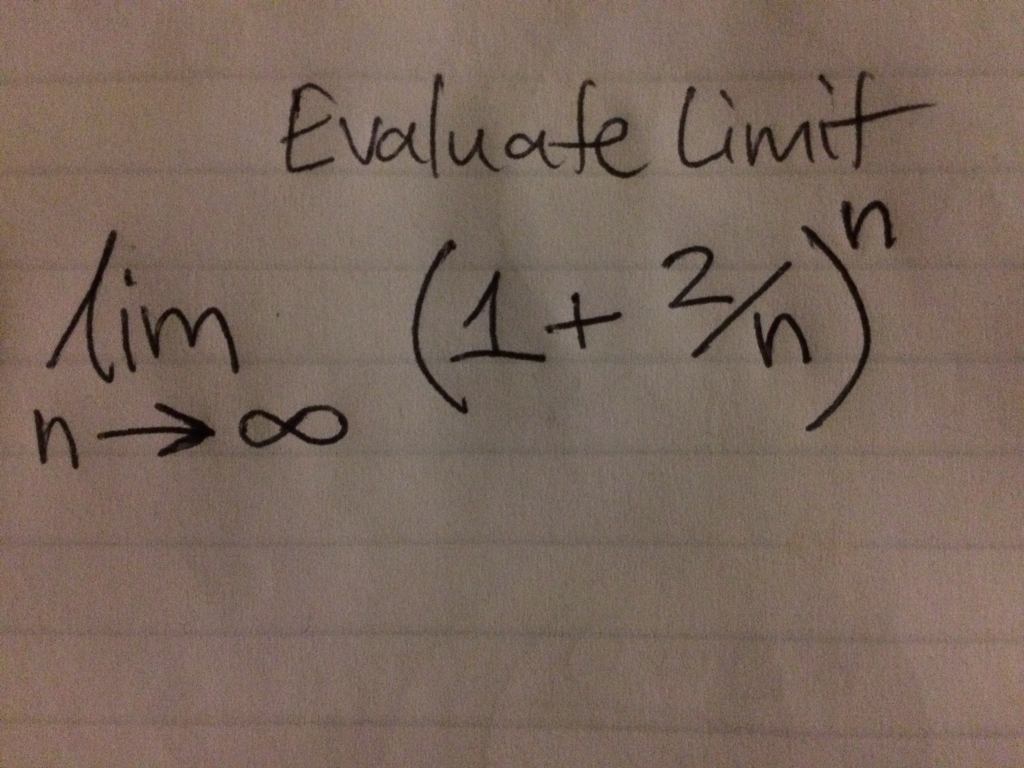



Evaluate Limit Lim N Rightarrow Infinity 1 2 N N Chegg Com



Solved Consider The Series C 1 N 2n N 1 Where Cis A Constant For Which Values Ofc Will The Series Converge And For Which It Diverge Course Hero
Weekly Subscription $199 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year until cancelledA term of the form f ( n) g ( n) can usually be converted to a L'Hopital's rule form by taking the log of both sides d n = 2 lim n → ∞ d n = e 2 ( 1) = 2 No need for L'Hopital, just the definition of the derivative Exponentiating back gives e 2 for the limitGiá trị của A = lim 2n23n1 3n2−n2 A = l i m 2 n 2 3 n 1 3 n 2 n 2 bằng Câu hỏi trong đề 75 câu trắc nghiệm Giới hạn cơ bản !!



Www Mtholyoke Edu Courses Jmorrow Calculus Ii Factexsolns Pdf



Http Www Math Colostate Edu Clayton Teaching M115f09 Exams Exam1solutions Pdf
Related Questions limπ→∞⋯⋯n99n100= EAMCET 1994 9100 1100 19;\displaystyle\lim_{{{n}\to\infty}}\frac{{\cos{{\left({n}^{{3}}\right)}}}}{{{2}{n}}}\frac{{{3}{n}}}{{{6}{n}{1}}}=\frac{{1}}{{2}} Explanation The limits of both$\begingroup$ @gaurav At that link you will find other methods that can be applied here For example, when $(a_n)$ is a sequence of positive numbers such that $\lim_n \frac{a_{n1}}{a_n}$ exists, then $\lim_n \sqrtn{a_n}$ exists and $\lim_n \sqrtn{a_n}=\lim_n \frac{a_{n1}}{a_n}$



Www3 Nd Edu Dgalvin1 S08 Exam3 Practice Solns Pdf



Link Springer Com Content Pdf 10 1007 2f978 3 7091 6146 3 12 Pdf
Evaluate lim(n→∞) {(n^6 6n^5 12n^4 1)^1/3 – (n^4 4n^2 6n 1)^1/2} asked in Limit, continuity and differentiability by Raghab ( 504k points) limits(a) Prove that lim n!1 n 2n = 0 You may use the fact that the inequality (1 x)n n(n 1) 2 x2 holds for all n 1 and x > 0 Solution Taking x = 1 in the inequality mentioned in the question gives 2n n(n 1) 2;> 0/math for all mathn \in \mathbb{N}/math So, math\dfrac{2^n}{n!} > 0/math for



1




Mth3101 Advanced Calculus Chapter 2
My Patreon page https//wwwpatreoncom/PolarPie as a limit using Squeeze Theorem https//wwwyoutubecom/watch?v=hLWCHRhVeA&t=13sW/O Squeeze Theorem httIIT JEE 12 Determinants 5 If the sum of n terms of an AP is given by S n = n 2 n, then the common difference of the AP is KCET 6 The locus represented by x y y z = 0 is KCET 18 Three Dimensional Geometry 7 If f (x) = sin − 1 ( 2 x 1 x 2), then f' ( 3) isIt is easier to work with limits involving powers when the base is the sum of math1/math and something else To do this, factor out math3^n/math mathL=\displaystyle\lim_{n\to\infty}(3^n2^n)^{\frac{1}{2n}}/math math\implies L=\displ



2



Http Darkwing Uoregon Edu Anderson Math315 Class2 Pdf
(n1)(n2) (n1)3 = lim n→∞ n2 n3 = 0 Therefore, the alternating series test implies P (−1)n(n1)(n2) (n1)3 converges 10 Since nn n!L'Hospital's Rule states that the limit of a quotient of functions is equal to the limit of the quotient of their derivatives lim n → ∞ n 2 n = lim n → ∞ d d n n d d n 2 n lim n → ∞ n 2 n = lim n → ∞ d d n n d d n 2 n Find the derivative of the numerator and denominator Tap for more stepsLimx → ∞ ( 2x3 − 2x2 x − 3 x3 2x2 − x 1 ) Go!



Ism Et Chapter 8




Determine Whether The Series Sum N 1 Infty 1 N 1 Frac 1 N N 2 Converges Absolutely Or Converges Conditionally Or Diverges Mathematics Stack Exchange
(x 2)n Using the Ratio Test, lim n!1 3n1e6(x 2)n1 (n 1)!By doing so, I get that 1/2 n converges at 1/2 Is this correct?Diverges 11 For all n > 2, we have n!



Www Math Uh Edu Almus 43 An Part2 Pdf



Math 414 Real Analysis Assignments
Is there an easier way?Click here👆to get an answer to your question ️ n→∞lim 1^22^23^2n^2/n^3 is equal toExample 2 lim n→∞ 3n4 −2n2 1 n5 −3n3 = 0 lim n→∞ 1−4n7 n7 12n = −4 lim n→∞ n4 −3n2 n2 n3 7n does not exist Pinching Theorem Pinching Theorem Suppose that for all n greater than some integer N,




Section 10 6 Recall From Calculus Lim Lim Lim X Y X X X Kx K 1 Y Y Eekek Let Y Kx In The Previous Limit Ekek If Derivatives Ppt Download




Stolz Cesaro Theorem Online Presentation
∫π2−π2 log2−sin θ2sin θdθ= 0 1 2 None of these Since fIs not zero and hence the series P (−1)nn n!Find the limit (lim n>infiniti) (n ∑ i=1) (2i/n)(2/n) Expert Answer Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculator




Limit Replace 1 By 0 Mathematics Stack Exchange



Link Springer Com Content Pdf 10 1007 2f978 3 7091 6146 3 12 Pdf
= n n n n− 1 n n− 2 ··n 2 n 1 > 1, the limit limn→∞ (−1)nn n n!(n23n6)2 n n4 = lim n!1 2n 3 (n2 3n 6)2 n4 n = lim n!1 2n 3 n n4 (n2 3n 6)2 = 2 1 = 2 Therefore, since the limit is nite and the series P n n4 = 1 n3 converges, the Limit Comparison Test implies that the given series converges as well 16For which values of xdoes the series X1 n=0 (x 4)nLimits of Sequences, Lim We already know what are arithmetic and geometric progression a sequences of values Let us take the sequence a n = 1/n, if k and m are natural numbers then for every k m is true a k > a m, so as big as it gets n as smaller is becoming a n and it's always positive, but it never reaches null In this case we say that 0 is



Search Q Limit Rules Tbm Isch




Poisson Limit Theorem Wikipedia
The value of n → ∞ lim 2 n sin 2 n a for a = 0 is equal to View solution The value of the n → ∞ lim n 2 1 n 2 − 1 1 n 2 − n 2 1 n 2 − ( n − 1 ) 2 1 is




Evaluate Lim N 1 N 1 N 1 1 N 2 1 3n Youtube




Show That Lim N Tends To Infinity 1 N 1 N 1 1 N 2 1 3n Log 3 Brainly In



What Is The Limit Of N Infinity N 2 N Quora



Faculty Math Illinois Edu Randy Ma231sp14 Ws9 Math231 Sol Pdf
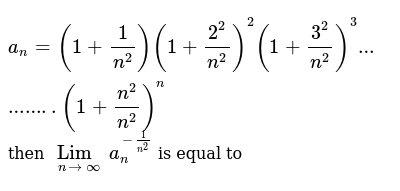



A N 1 1 N 2 1 2 2 N 2 2 1 3 2 N 2 3 1



Determine The Convergence Of The Series 1 N Arctan 1 2n 1 Stumbling Robot




N Ool An 2 2n 2 Limm 2n 1 2n Lim 00 2n 1 2 2n Nag 2n 1 2n N 00 N 1n Lim The Ratio Test Exercises Test Meme On Me Me



Www Toppr Com Ask En Ae Question For Ain R The Set Of All Real Numbers Aneq 1 Lim Nrightarrow Infty




Ex 7 8 4 Integrate X2 X Dx By Limit As A Sum Ex 7 8




Sequences And Series Pdf Free Download




Answered S 1 Is N N 1 Convergent Divergent Check Bartleby




Example 25 Find Integral X2 1 Dx As Limit Of A Sum Examples




Lim N Oo 1 2 2 2 3 2 N 2 N 3 Is Equal To A 1 B C 1




6 1 3 Areas As Limits Of Riemann Sums
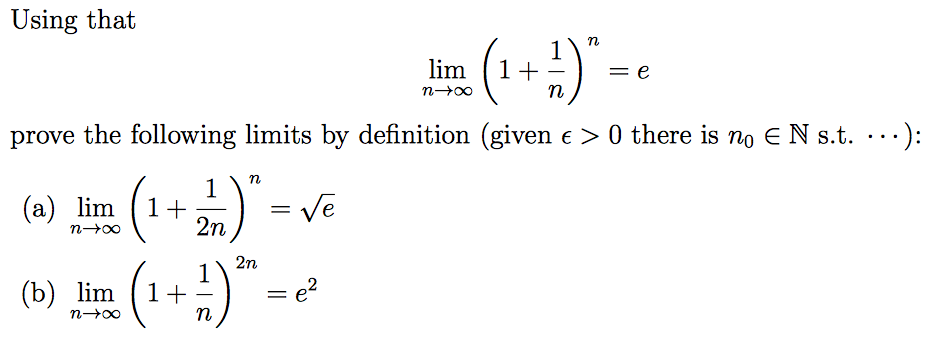



Using That Lim N Rightarrow Infinity 1 1 N N E Chegg Com




2 Prove That Lim 1 1 0 72 00 N 2n 3 Prove That Lim Noon 1 Homeworklib




極限クイズ Lim N 2n N N N 1 N Clear




Solved Lim N Tends To Infinity 1 2 3 1 3 4 1 N N 1 Equals Brainly Com



Www Colorado Edu Amath Sites Default Files Attached Files Archive Appm1360summer18exam3 Sol Pdf




Ism Et Chapter 8
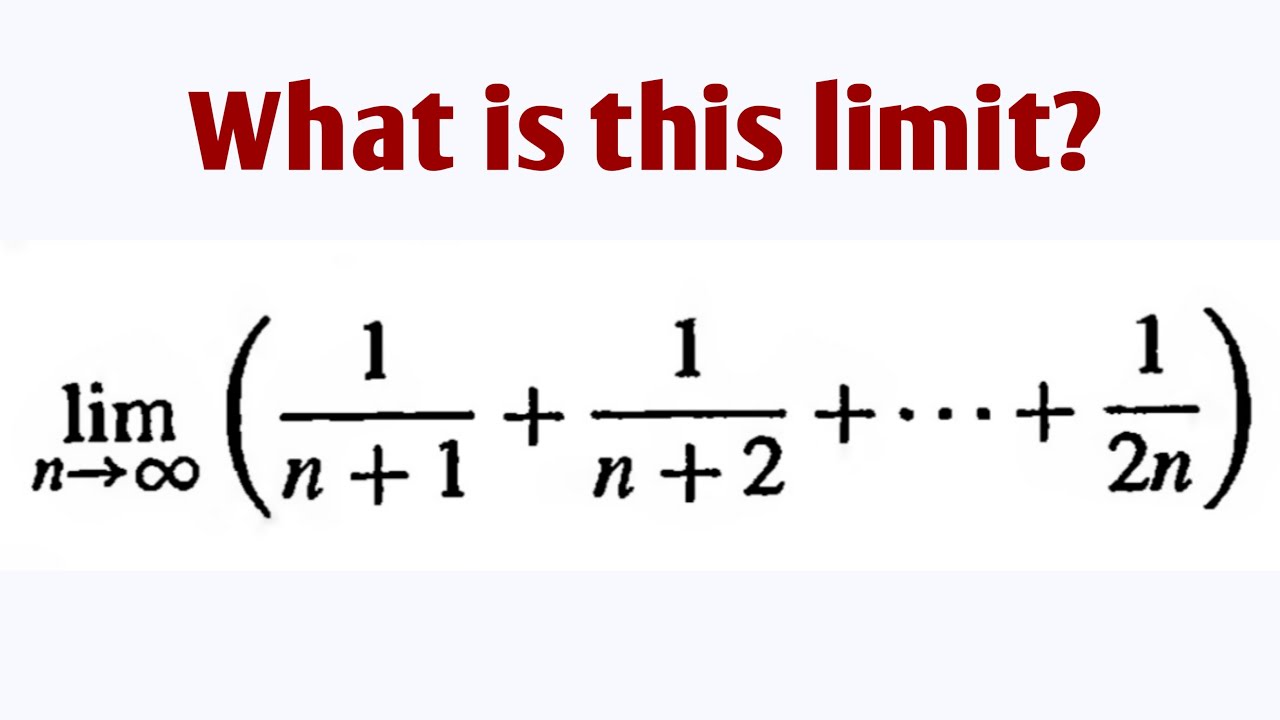



Lim 1 N 1 1 N 2 1 2n What Is This Limit Youtube




Lim N Tends To Infinity 1 2 2 2 N 2 N 4 Brainly In




F X Dx Hence The Valladio Ui Find R2 1 R 1 Dx As




6 1 3 Areas As Limits Of Riemann Sums
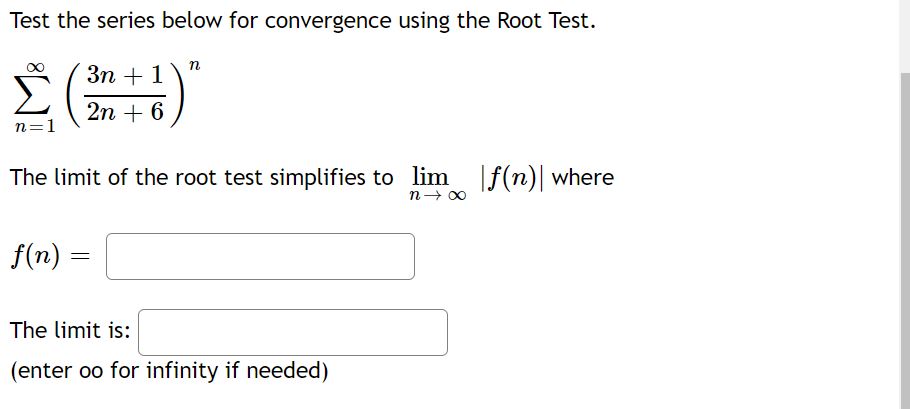



Answered Test The Series Below For Convergence Bartleby




A Limit Involving Binomial Coefficients Lim N To Infty 1 N Sum K 1 N 1 K N Choose K 1 K Frac12 Mathoverflow
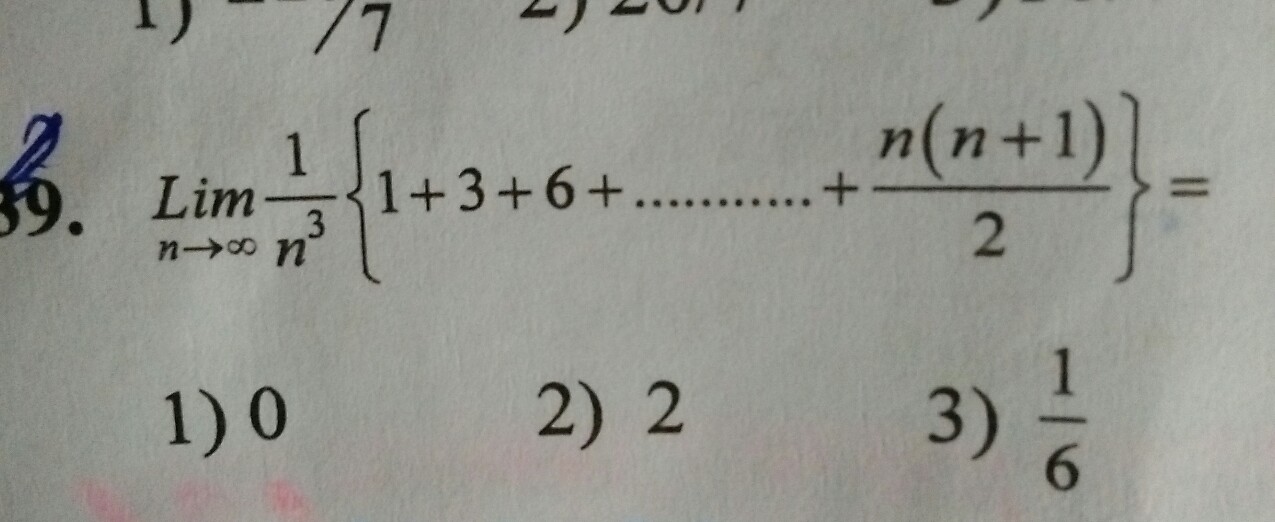



Lim N Infinity 1 N 3 1 3 6 N N 1 2




Lim N 2 N 1 N 2 N 1 N N 1 N Is Infinity Askiitians




Take For Granted That The Limit Lim 1 1 N N Chegg Com



2



Search Q Limit N Tends To Infinity 1 N Tbm Isch
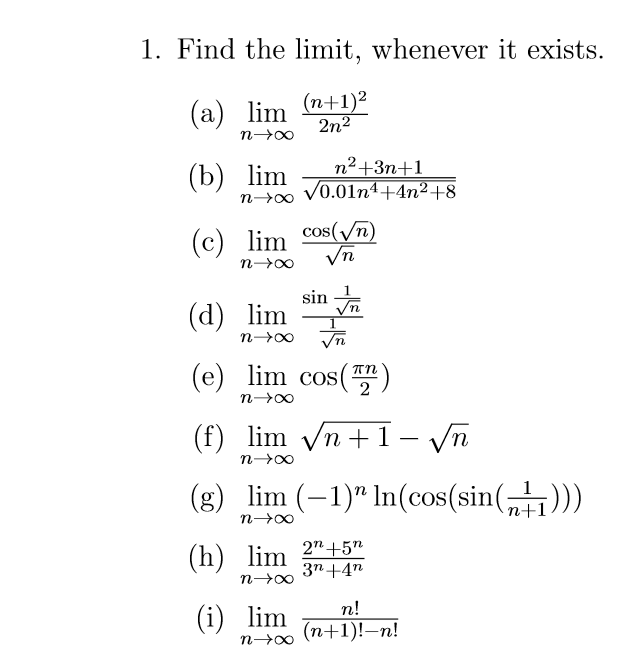



Find The Limit Whenever It Exists A Lim N Chegg Com




Ma2108s Tutorial 5 Solution




Math 121 Homework 7 Solutions




Chapter 1



Www Jstor Org Stable



1
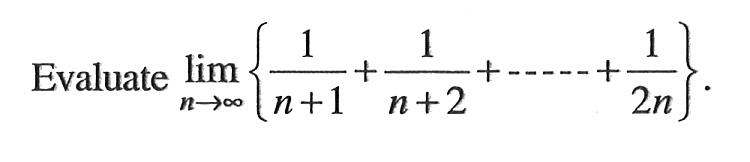



Evaluate Lim N 1 N 1 1 N 2 1 2n Mathematics 1 Question Answer Collection




Science Infinite Series Module Units Unit 1 1 1 Infinite Sequences 1 1 06 Limit Laws Example Ubc Wiki




Proof Of Lim N To Infty Sqrt N N 1 Mathematics Stack Exchange



Determine The Convergence Of The Series 1 N N 1 2 N100 2n Stumbling Robot
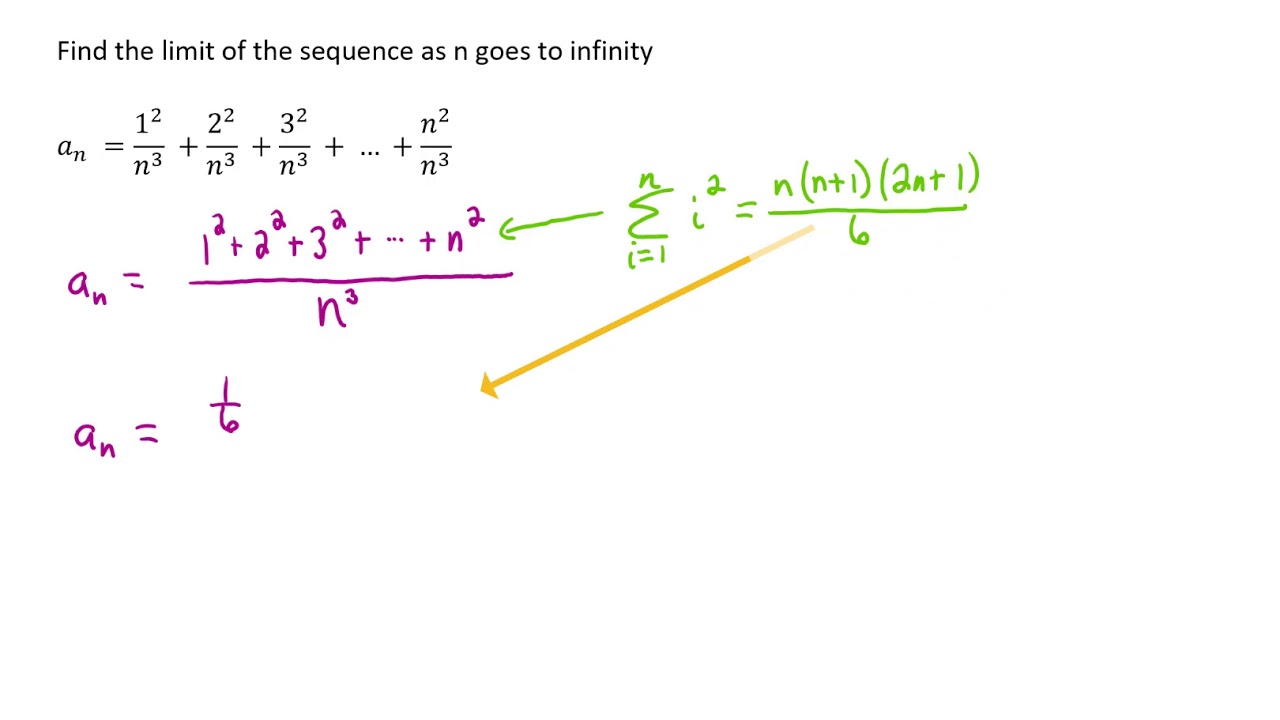



Find The Limit Of 1 N 3 2 2 N 3 3 2 N 3 N 2 N 3 As N Goes To Infinity Sequences 2 Youtube
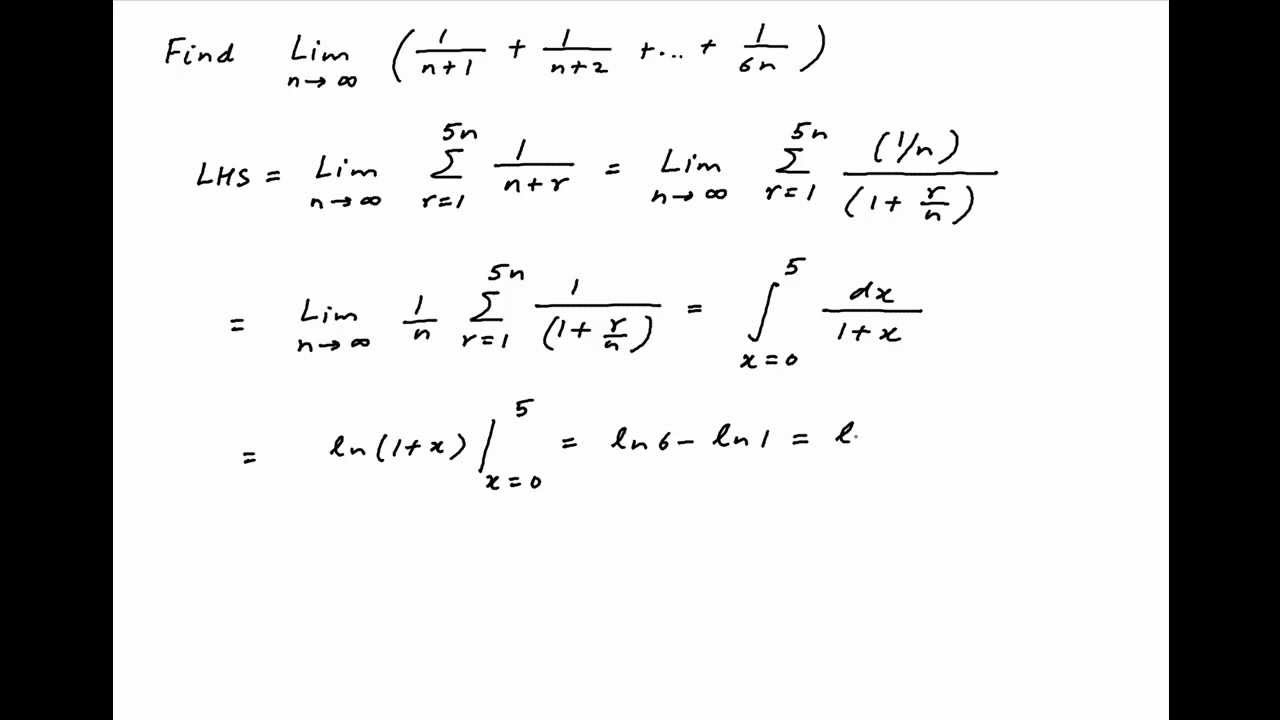



Find The Limit Of 1 N 1 1 N 2 1 N 3 1 6n As N Tends To Infinity Youtube



Lim N N 1 N 2 3n N 2n 1 N Is Equal To Sarthaks Econnect Largest Online Education Community



Users Math Msu Edu Users Yanb 3hw2 Key Pdf



Http Users Math Msu Edu Users Lawrence 3 Hmwk3 Solns Pdf




Log B Log A Log Bla N 1 N 2 N




Video 2533 Limit Of Sequence 1 1 N 2 N Practice Youtube



Www Ualberta Ca Rjia Math214 Hwks Sol2 Pdf




Science Infinite Series Module Units Unit 1 1 1 Infinite Sequences 1 1 06 Limit Laws Example Ubc Wiki
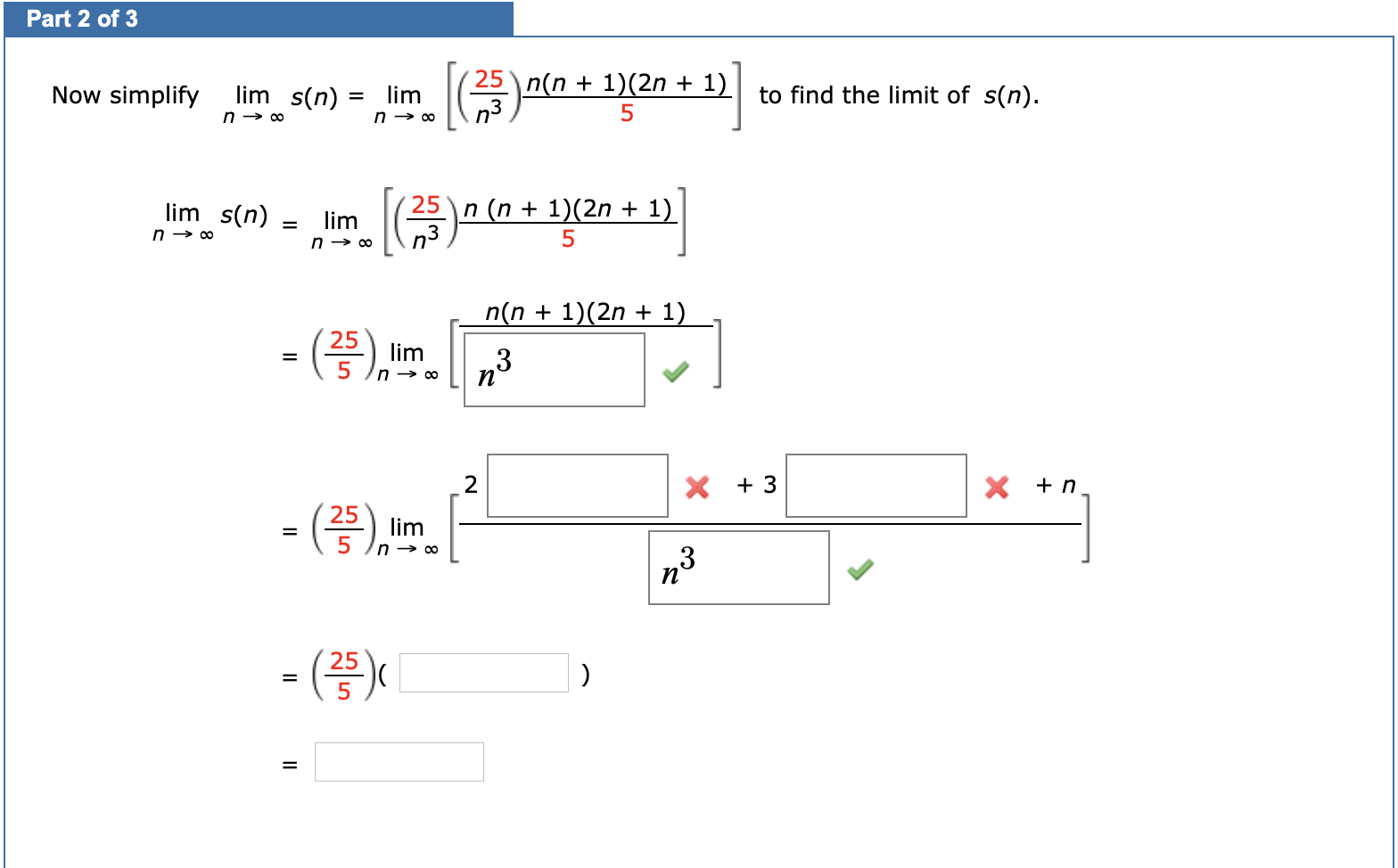



Answered Now Simplify Lim S N Lim N 0 25 N N Bartleby




Evaluate Lim N 1 N 1 1 N 2 1 2n Youtube




Lim N Oo 1 N 2 N 1 3 N 2 N 1 1 2 2 2 3 2 N 2
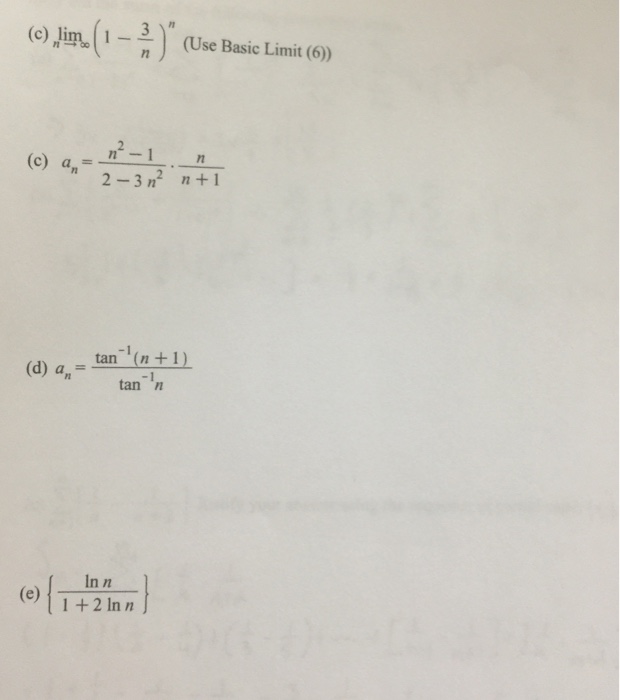



Lim N Rightarrow Infinity 1 3 N N Use Basic Limit Chegg Com




Telescoping Series Wikipedia



Http Www D Umn Edu Jgreene Honors calculus Exam 3 11 Sol Pdf




I Lim N Infinity Pn 2 N Ii Lim X Infinity A 1 X B 1 X C 1 X 3 X



Http Www Math Sci Hokudai Ac Jp S Settepanella Teachingfile Calculus Calculus1 Pagine Exthpag28 32 Pdf




Prove The Following Using The Definition Of A Limit Chegg Com




Math 101 Homework 2 Solutions 1 Evaluate The Limits N




Calculus Find The Radius Of Convergence For 3n Online Presentation




Lim N Infinity N N 2 1 Youtube




Evaluate Lim N 1 N 1 1 N 2 1 2n Mathematics 1 Question Answer Collection




Last Lecture In Infinite Series




N Ool An 2 2n 2 Limm 2n 1 2n Lim 00 2n 1 2 2n Nag 2n 1 2n N 00 N 1n Lim The Ratio Test Exercises Test Meme On Me Me
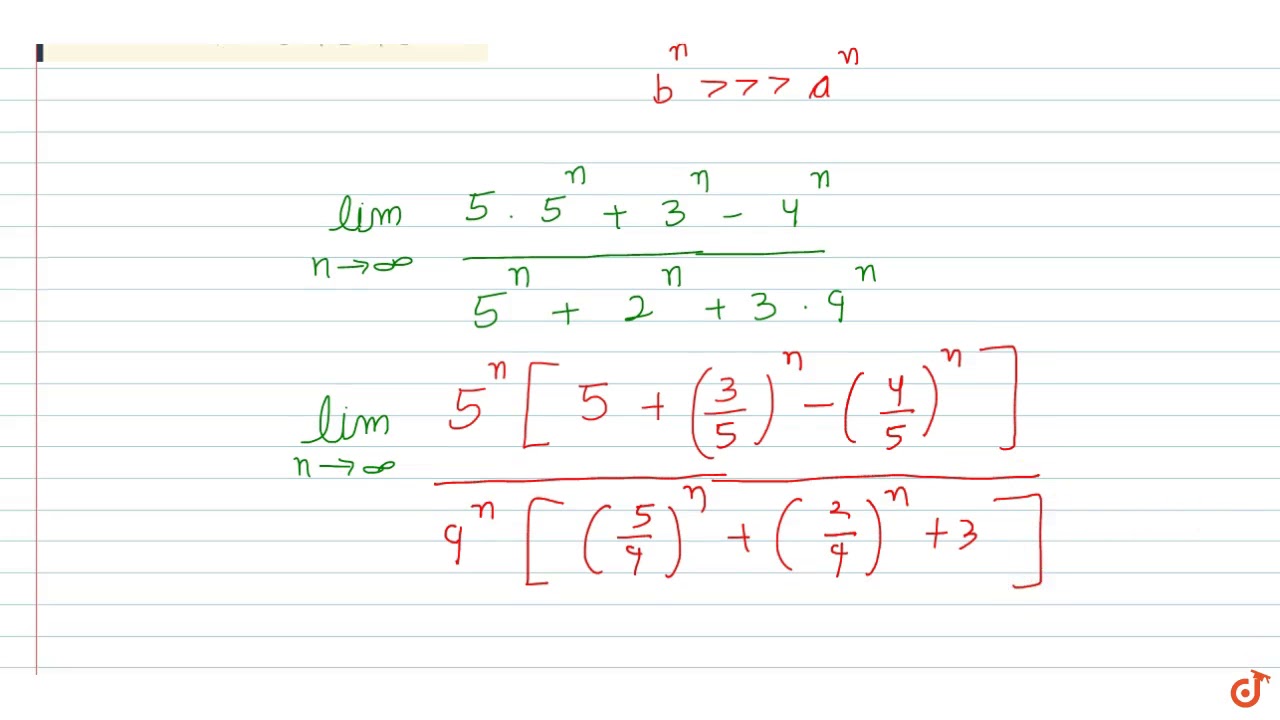



Lim N Gtoo 5 N 1 3 N 2 2n 5 N 2 N 3 2n 3 Youtube




What Is Math Lim Limits N To Infty Left 1 Frac 1 N Right N Math Quora




1 Use The Definition Of Limit To Show That Lim 2n 1 Chegg Com




Chapter 3 Cbu



Limit Of Sequence Lim N 1 Cos 2 N Physics Forums



0 件のコメント:
コメントを投稿